No sabía esto, investigaré al respecto.
Gracias.
No sabes muchas cosas Omnio, aunque curiosamente te pasas el 99% de tu tiempo aquí intentando opinar y debatir sobre ellas 
Xoso, xoso, si de verdad te jode tanto que sepa más que tú lo lamento, simplemente nací con el don de la inteligencia bastante más allá que el resto.
Como breviario cultural, la palabra inteligencia proviene del latín intellegentĭa y es la capacidad de entender, asimilar, elaborar información y utilizarla para resolver problemas.
ESTE CLON ES EXTRAORDINARIO





 representa la incógnita, mientras que el coeficiente 3 y los números 1 y 9 son constantes conocidas. La igualdad planteada por una ecuación será cierta o falsa dependiendo de los valores numéricos que tomen ambos miembros; se puede afirmar entonces que una ecuación es una igualdad condicional, en la que solo ciertos valores de las variables la hacen cierta.
representa la incógnita, mientras que el coeficiente 3 y los números 1 y 9 son constantes conocidas. La igualdad planteada por una ecuación será cierta o falsa dependiendo de los valores numéricos que tomen ambos miembros; se puede afirmar entonces que una ecuación es una igualdad condicional, en la que solo ciertos valores de las variables la hacen cierta.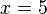



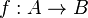 y un elemento
y un elemento  del conjunto
del conjunto  , resolver una ecuación consiste en encontrar todos los elementos
, resolver una ecuación consiste en encontrar todos los elementos  que verifican la expresión:
que verifican la expresión:  . Al elemento
. Al elemento  se le llama
se le llama  que verifique
que verifique  .
. son funciones y la aplicación
son funciones y la aplicación  debe incluir alguna de las derivadas del argumento. En las ecuaciones matriciales, la incógnita es una matriz.
debe incluir alguna de las derivadas del argumento. En las ecuaciones matriciales, la incógnita es una matriz. , pues, si
, pues, si  es un grupo basta con definir la aplicación
es un grupo basta con definir la aplicación  y la ecuación se transforma en
y la ecuación se transforma en  .
. , donde
, donde  es la
es la  es el conjunto vacío, la ecuación no es soluble; si tiene sólo un elemento, la ecuación tendrá solución única; y si
es el conjunto vacío, la ecuación no es soluble; si tiene sólo un elemento, la ecuación tendrá solución única; y si  . Una
. Una  un polinomio, se tiene
un polinomio, se tiene  tiene alguna topología. No es el único: en los sistemas de ecuaciones reales, se recurre a técnicas algebraicas para averiguar si el sistema tiene solución. No obstante, el álgebra parece que carece de recursos siquiera para asegurar la existencia de soluciones en las ecuaciones algebraicas: para asegurar que toda ecuación algebraica con coeficientes complejos tiene una solución hay que recurrir al análisis complejo y, por lo tanto, a la topología.
tiene alguna topología. No es el único: en los sistemas de ecuaciones reales, se recurre a técnicas algebraicas para averiguar si el sistema tiene solución. No obstante, el álgebra parece que carece de recursos siquiera para asegurar la existencia de soluciones en las ecuaciones algebraicas: para asegurar que toda ecuación algebraica con coeficientes complejos tiene una solución hay que recurrir al análisis complejo y, por lo tanto, a la topología.


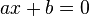
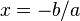
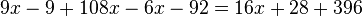
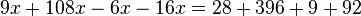
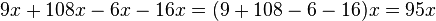
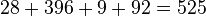

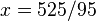


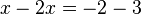


 siempre se tienen dos soluciones:
siempre se tienen dos soluciones:
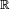 se requiere que
se requiere que  y para que tenga soluciones sobre los números racionales
y para que tenga soluciones sobre los números racionales  se requiere
se requiere  .
.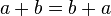 para toda
para toda  y
y  ), y es así el primer paso al estudio sistemático de las propiedades del sistema de los
), y es así el primer paso al estudio sistemático de las propiedades del sistema de los 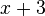


 . Los valores de las variables que hacen la ecuación verdadera se llaman las soluciones de la ecuación.
. Los valores de las variables que hacen la ecuación verdadera se llaman las soluciones de la ecuación. .
.

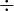 :
:

![<br />
\sqrt{a} \; ; \quad<br />
\sqrt[b]{a}<br />](http://upload.wikimedia.org/math/d/3/d/d3d2d632cabc0bc05a8afc4f29e06e57.png)

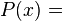



 , que es igual a sumar un
, que es igual a sumar un 

 ó
ó 


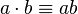
 , que es igual a multiplicar por el
, que es igual a multiplicar por el 



 (n veces)
(n veces) y
y 
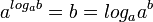
![\ a^{m/n} \equiv (\sqrt[n]{a^{m}})](http://upload.wikimedia.org/math/9/d/c/9dce189c9cd5c2644b62a96c54e7eb83.png) y por lo tanto las raíces pares de números negativos no existen en el sistema de los números reales. (Ver:
y por lo tanto las raíces pares de números negativos no existen en el sistema de los números reales. (Ver: 

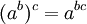

 entonces
entonces 
 entonces
entonces 
 entonces
entonces  y
y 

 y
y  no es cero, entonces
no es cero, entonces  y
y  entonces
entonces 
 entonces
entonces 
 entonces
entonces 
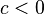 entonces
entonces 













No sabía esto, investigaré al respecto.
Gracias.
No sabes muchas cosas Omnio, aunque curiosamente te pasas el 99% de tu tiempo aquí intentando opinar y debatir sobre ellas
Xoso, xoso, si de verdad te jode tanto que sepa más que tú lo lamento, simplemente nací con el don de la inteligencia bastante más allá que el resto.
Como breviario cultural, la palabra inteligencia proviene del latín intellegentĭa y es la capacidad de entender, asimilar, elaborar información y utilizarla para resolver problemas.
Este tiene que ser Batch XDDDD