OcioCiencia 0.3

¡Hay más preguntas! ¡Cosmología, Cosmología, Cosmología!

Curioso ritmo el que llevamos, lo que salga del 0.1 va para el 0.3, y lo que salga del 0.2, supongo, irá para el 0.4. ¿A alguien más le parece que estamos siguiendo una superposición de las gráficas del seno y del coseno? Bueno, olvidadlo. Lo importante es que para esta entrega tenemos más preguntas, y nada menos que... ¡6! ¡Weeee! El valiente que ha lanzado semejante batería es Nelion, al cual agradezco mucho su interés, sus preguntas y sus halagos, y no necesariamente en ese orden, je. Empecemos, que aquí hay jugo para un zumito de OcioCiencia.

La verdad por delante, no podré responder con precisión a algunas preguntas, y no porque no sepa las respuestas sino porque algunas carecen de sentido. Pero no pasa nada, las comentamos y con eso revisamos aquellas ideas relativistas, ¿no? No es fácil adaptarse a una visión del universo en cuatro dimensiones, y dejar el tiempo ligado al espacio con todo lo que ello conlleva (aparentes paradojas y demás) lo hace aún más complicado. Pero, como dijera mi profe (vaya tío) “tenéis que dar el salto... aunque sea con colchoneta”. Venga, como montar en bici, que cuando uno se acostumbra ya no es para tanto.

Esto me recuerda otra cosa que nos dijo ese profe (hoy estoy nostálgico). Déjenme compartirlo con ustedes. Éramos sólo cuatro en clase (de un total de seis, pero sólo íbamos cuatro). Era viernes, la clase era de 13.30 a 14.30 y, a finales de Mayo, a esas alturas del curso y a esa hora no había ya casi nadie por la universidad. Pasó que acabada la lección dedicada a todo este rollo y con muchísimas formulitas, subíndices, numeritos y letras (incluyendo griegas), el profesor se giró entusiasmado a nosotros y dijo “esta teoría parece difícil pero no lo es”. Uno de nosotros le respondió “tiene mala fama”, y al momento repuso él alegremente “¡tiene mala fama!”. Luego hizo una pausa de unos cinco segundos y, tras ver nuestras caras, añadió “no es... para tanto” (ni me imagino cómo nos pusimos, pero parecía un velatorio). Y tras otros cinco segundos mirándonos, sentenció “yo creo, vamos”. Y se fue... asumiendo su culpa, supongo. Ya está, tenía que dejarlo escrito para que quedase constancia de aquello en alguna parte, y le ha tocado a esta web. Sigamos.

La primera pregunta dice así: Mencionabas que el universo siempre está aumentando, por lo tanto su geodésica también estaría variando constantemente, ¿no?

Aquí veo el problema de usar un lenguaje un poco ambiguo, porque quizás he usado la palabra universo para referirme a más de un concepto, y obviamente eso trae confusión. Para aclararnos, a partir de ahora llamaré universo al espacio-tiempo (esa cosa de 4 dimensiones), y cosmos a lo que es el espacio que se ve en las pelis galácticas. Entonces, observando ya la pregunta planteada debo decir que hay que tener cuidado con las conclusiones que sacamos. El espacio-tiempo no está creciendo, pues alberga todos los espacios en todos los tiempos posibles. Es como si considerásemos simultáneamente a una persona en su etapa infantil, juvenil, madura y senil. No puede crecer porque no pasa ningún tiempo para ella, ¡está en todas sus edades posibles a la vez!

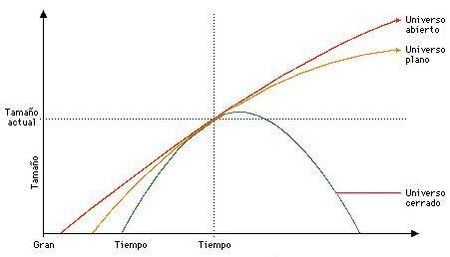
Ahora bien, lo que sí crece es el espacio respecto al tiempo. Se sabe que ahora mismo el cosmos está creciendo y... ¡nada puede pararlo! Je, no, qué va. Nos ponemos serios: se sabe que está creciendo pero no si lo hará siempre. Este detalle es importante. No todos los científicos creen que esta expansión vaya a ser interminable. Algunos se acogen a la llamada Teoría del Universo Pulsante, ya vista en el OcioCiencia inaugural. Este modelo, pese a que no parece el más acertado, aún no se puede descartar. Repetiré su idea: la visión general del universo sería como el acordeón de Maria Jesús y su baile de los pajaritos, que está expandido y contraído una y otra vez soportando infinitos Big Bang’s por toda la eternidad. En cada estiramiento/contracción lo que crece y decrece es el cosmos, no el universo. El espacio-tiempo lo abarca siempre todo, no puede crecer ni tampoco decrecer. ¿Y acaso no se dice que el universo aparece con el Big Bang? Pues sí, pero eso no significa que crezca. Una vez que ha surgido ni crece ni decrece. Estamos viendo el cosmos en todas sus épocas posibles a la vez. O al menos eso intentamos. Y sin usar drogas alucinógenas, que tiene más mérito.

En referencia a las geodésicas, aclararé un poco lo de “la geodésica del universo”, que hasta donde sé es una expresión incorrecta. Una geodésica es un concepto geométrico propio de un espacio (en nuestro caso, el universo de 4 dimensiones, y no le podemos quitar ninguna, ojito con quitarle la del tiempo, eh). Esas geodésicas son los caminos de mínima longitud para ir de un sitio a otro, y por ello no tiene por qué haber una única. Yo al menos no sé de ningún espacio que sólo tenga una geodésica, salvo un punto o un espacio unidimensional, en el que la geodésica es el espacio mismo. Lo que sí es usual es que haya un solo tipo de geodésica, como es el caso de un espacio plano (todas son rectas) o una esfera (todas son circunferencias máximas).

Pero ocurre que el espacio-tiempo no es una superficie bonita, sino que está tan, tan, tan... ¿que es una campana? ¡No! Nuestro universo lo que está es muy deformado por las estrellas, galaxias, agujeros negros y demás cuerpos (con una materia suficiente) que alberga. Eso sin mencionar que estamos en 4 dimensiones, y quizás haya unas 7 más, con lo que para viajar de un punto del universo a otro podrían existir lo que se denominan puentes de Einstein-Rosen o, más vulgarmente, agujeros de gusano. Voy a explicar esto último porque es interesante.

El gráfico siguiente, obra mía (lo siento, no logré hacerlo mejor), muestra una posible geodésica (pura conjetura) que pasaría por lo que es la garganta del agujero sin necesidad de ir por el camino usual en el caso de que dos puntos estuviesen simétricos y alejados respecto del plegado. Es como si el agujero de gusano fuera un atajo que permite viajar de un punto del cosmos a otro muy alejado. Pero el chiste no es que sólo nos permitiría viajar en el espacio sino en, no discriminemos, cualquier dimensión, y eso incluye el tiempo.

Con esto quiero decir que en el universo no hay un único tipo de geodésica, y como prueba, sin mencionar teorías poco contrastadas ni agujeros ni gusanos, basta ver que Marte sigue una trayectoria elíptica mientras que aquellos cometas que sólo visitan una vez nuestro sistema solar describen una órbita hiperbólica.

Ahora bien, aunque no hay un único tipo de geodésica, para cada cuerpo sí hay una geodésica. Las cosas en el universo no se mueven por donde les da la gana, se mueven por el único sitio por donde pueden ir. Imaginaos la caída libre de una bola por una rampa. ¿Puede elegir hacia donde moverse? No, no puede, y lo mismo les pasa al resto de cosas que viajan en el espacio-tiempo.

¿Y cómo sabemos que no hay un único tipo de geodésica? Porque al compararlas vemos que no son iguales. Hay una variación de unas respecto a otras que se mide con la curvatura intrínseca del espacio-tiempo. Sobre esta curvatura actúan varios factores y gaitas que ni algunos científicos entienden, y es mejor que no profundicemos en ellas (se escapa de mis modestos límites, la verdad), pero sí podemos mencionar que para hallarla se usa una métrica. Métricas hay muchísimas, pero la métrica más famosilla es la de Robertson-Walker que, junto a las ecuaciones de Friedman, saca diferentes modelos del universo que nos plantean qué tipos de geodésicas presentará. Así tenemos el modelo de Einstein-DeSitter que nos dice que el cosmos se expande proporcionalmente al cuadrado de la raíz cúbica del tiempo mientras que otros, como el modelo de Milne, afirma que la expansión es directamente proporcional al tiempo... Como curiosidad, decir que todos esos modelos anuncian que, como mínimo, una vez se produjo un Big Bang.

Pasemos a la siguiente pregunta: ¿Influiría también en las geodésicas de los demás cuerpos (planetas, estrellas, etc.)?

La respuesta de esta pregunta está dada en la anterior (las letras en negrita de los párrafos anteriores). Lo importante es quedarse con la idea de que no sólo las geodésicas guían a los cuerpos, sino que los cuerpos deforman al espacio gracias a su materia (que no masa).

Así, los cuerpos más densos (gran concentración de materia) “tiran” del espacio-tiempo hasta que llegan a colapsarse convirtiéndose en agujeros negros que, debido a sus grandes densidades, absorberían cualquier cosa (hasta la luz) en un radio cercano. Y como la luz no puede escapar, nada escapa de ellos, ya que en Relatividad nada va más rápido que la luz. Usualmente se piensa que un agujero negro surge a la muerte de una estrella cuando supera el límite de Chandrasekhar, pero la verdad es que según lo que acabamos de decir cualquier cosa podría convertirse en un agujero negro al pasar un cierto límite. Claro que el hecho de que uno de nosotros pueda transformarse en un agujero negro y tragón es más difícil que hacer gárgaras boca abajo, porque para ello me parece (ahora sí hablo de memoria) que el objeto aspirante debería alcanzar tanta materia como el doble de su radio (en un sentido más complejo que el dado a una circunferencia) para empezar a autocolapsarse. Y hablando de esto, se rumorea que en el centro de nuestra galaxia existen las condiciones adecuadas para que haya un agujero negro muy simpático y gordo (sobre todo esto último) haciendo de las suyas.

Y mírala cara a cara que es la tercera: En referencia a que no existe la gravedad, el hecho de que los cuerpos del espacio parezcan mantener una posición siempre igual entre ellos (me refiero al hecho de que la Luna siempre esté a la misma distancia de la Tierra, por ejemplo), ¿se explicaría por la atracción, digamos, magnética?

De seguro que el electromagnetismo y la interacción gravitatoria tienen algo que ver, pues son dos de las cuatro fuerzas fundamentales que hay dando la tabarra. Pero siguiendo la línea que llevamos nos podemos fijar en las consecuencias más que en los motivos: si algo gira alrededor de la Tierra es porque está cayendo continuamente hacia ella. Por tanto la Luna sigue una geodésica dada por la curvatura de esa región y las densidades de ambos cuerpos (satélite y planeta), y esa geodésica tiene “atrapada” a la Luna. Es decir, no puede seguir otro camino que no sea el de girar una y otra vez (a no ser que pase por allí algún enorme meteorito para tambalearlo todo). Por tanto no hay que inventarse ninguna gravedad para explicar el giro de la Luna, es esa curvatura no visible pero sí detectable (como el fenómeno de juntar dos imanes con misma polaridad) lo que en última instancia hace mover a la Luna lunera cerca de nuestro planetita.

Genial, Luc, eso ha quedado genial, ¿pero por qué si el cosmos está en expansión no se separan los planetas de nuestro sistema solar? Bueno, porque el Sol ejerce una curvatura en el espacio-tiempo muy fuerte y le grita al resto “vosotros conmigo” mientras que el cosmos sólo susurra “seguidme”. Es análogo al hecho de coger hojas de un árbol y ponerles encima piedrecitas. Si las echamos en un lago veríamos que las hojas se alejan unas de otras, cual galaxias, pero las piedrecitas que llevan encima no se alejan de las hojas sino que van con ellas, como los sistemas solares respecto a las galaxias, los planetas respecto a las estrellas y los satélites respecto a los planetas.

Venga, la cuarta que podemos: ¿Cómo influye la energía en las geodésicas de los cuerpos?

Primeramente el espacio le “dice” a la materia qué geodésicas seguir. Pero, eh, aquí está la respuesta: es que, como ya hemos dicho, a su vez la materia actúa sobre el espacio y le “dice” cómo curvarse, describiendo juntitos las geodésicas que se pueden dar. Sí, sé lo que cabe preguntarse ahora. He dicho materia cuando en la pregunta se hablaba de energía, pero es que en Relatividad, por la famosa ecuación de Einstein, hay una equivalencia masa-energía (donde masa se refiere a masa relativista), luego la energía influye en las geodésicas. Todo influye en todo. Desde el sistema Alfa Centauri en nuestro Sol hasta nuestro Dolby Surround en la casa del vecino. En nuestra realidad los sistemas aislados no se dan, y de darse nunca los podríamos conocer ya que al verlos, con sólo nuestra presencia, ya los estaríamos modificando y ya no serían aislados. Esto último es el principio de incertidumbre de Heisenberg.

Volviendo a la pregunta, vale, la energía influye en las geodésicas, ¿pero cómo? Ojalá lo supiéramos. Me temo que esta pregunta está por resolverse, y el camino para hallar su respuesta parece largo. ¿Hay prisa? Algo sí se sabe, y es que al ir por las geodésicas los cuerpos siguen trayectorias de mínima longitud, y eso está relacionado con la función de energía. Lo que sabemos desde el cole: para ir de un sitio a otro, como menos esfuerzo y tiempo empleamos es viajando en línea recta pues cuando estamos sobre la Tierra a corta distancia la vemos como un plano.

La quinta y sexta, de golpe: Y más aún, si la geodésica del universo aumenta debido a que el universo siempre está en aumento, ¿no debería aumentar también la energía necesaria para su movimiento? Y en tal caso, ¿de dónde procedería?

Entre “la geodésica del universo” y “el universo siempre está en aumento”, estas dos cuestiones casi no se dejan meter mano (y eso que somos decentes, ¿no?). Verás, las geodésicas del universo no aumentan, lo mismo que no aumenta el universo. Se puede pensar que cuando el cometa Halley se va de marcha está “esforzándose” para viajar, pero no es así. Simplemente va por donde puede. Ningún cuerpo se mueve porque esté en una carrera, ¡se mueve porque no hay nada que lo mantenga quieto! ¡Debería esforzarse para detenerse, no para corretear! En nuestra experiencia, ¿cuándo se mueve algo por sí solo? Cuando se está cayendo. Luego en el cosmos todo está cayendo continuamente.

Sé lo que estáis pensando (suponiendo que aún seguís conmigo): ¿y cómo es que el cometa Halley “cae” si no hay gravedad? Es que no hay gravedad en ningún sitio, ni siquiera en la Tierra. Esto lo deberíamos aceptar, asumir y comprender. ¿Quién ha experimentado la gravedad alguna vez? Nadie. El que se tiró de un puente lo que experimentó fue el cemento interponiéndose en su geodésica. En el universo no hay nada que diga “tu pa’ abajo”. Sería absurdo, en el universo no hay arriba ni abajo, ni derecha ni izquierda. Todos eso es relativo. Cuando te pones frente a un amigo, tu izquierda es su derecha, y su derecha es tu izquierda. ¿Quién lleva razón? ¡Los dos por separado y ninguno a la vez! Depende del punto de vista, porque tu orientación siempre estará fija respecto a ti, y no respecto a un marco de referencia externo que, sencillamente, en Relatividad no se puede encontrar. Lo importante es saber que seguir la geodésica es el movimiento natural de un cuerpo y, sobre todo, si no hay nada que lo frene, no se va a frenar nunca.

En fin, esto ha sido todo por ahora. Al que se lo haya leído enterito, mi enhorabuena. Al que se lo haya leído enterito y sin hacer pausas, le doy la mano. Y por el que se lo haya leído enterito, sin hacer pausas y lo haya comprendido de cabo a rabo, me quito el sombrero. Por mi parte, espero haber cumplido con los pronósticos. Si no, como decía aquel, “puedo volver a explicárselo hasta que definitivamente no lo entienda”. Pero sinceramente han sido unas cuestiones muy, muy buenas las que nos ha dejado el amigo Nelion. A mí me habían planteado bastantes (en fiestas familiares en plan “vamos a escuchar al desquiciado”) y normalmente se repetían, pero aquí hay algunas que me han hecho vacilar cómo enfocarlas.

Anímense y dejen sus preguntas por aquí para que puedan verlas mis informadores y me den trabajito. Háganlo sin ningún pudor, que el plantear preguntas es una buena forma de aprender. Piensen que por cada una que me hagan, yo les hice a mis profesores cuatro. Según este artículo, habría hecho veinticuatro y… tanto creo que no. No obstante yo, como Newton, “he sido un niño que jugando en la playa encontraba de tarde en tarde una concha más bonita de lo normal, contemplando cómo el océano de la verdad se extendía, inexplorado, delante de mí”.